Ý tưởng
Kiểm định chi bình phương về tính độc lập bằng cách so sánh tần số quan sát được trong các ô với tần số bạn mong đợi nếu không có mối liên hệ giữa hai biến danh nghĩa. Vì các tần số mong đợi được dự đoán trên không có mối liên hệ nào, mối liên hệ giữa hai biến danh nghĩa càng lớn, bạn càng mong đợi các tần số quan sát khác với tần số dự kiến. Hai biến danh nghĩa càng ít liên kết với nhau, thì tần số quan sát được sẽ càng gần với tần số mong đợi.
Để xem toàn bộ nội dung bài viết, vui lòng truy cập link sau: https://ungdung.hotronghiencuu.com/kiem-dinh-tinh-doc-lap-cua-2-bien-dinh-danh
Kiểm định cặp giả thuyết sau
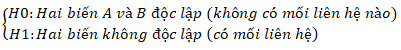
Tính thống kê chi-square
Trong đó O là giá trị quan sát và E là giá trị kỳ vọng trong mỗi ô
Với r là số danh mục của biến ở hàng, c là số danh mục của biến ở cột, tích (r-1)*(c-1) gọi là số bậc tự do của kiểm định khi bình phương.
Khi thực hiện trên SPSS ta có thể nhìn vào giá trị sig. Nếu sig <α ta bác bỏ H0
Thực hành với SPSS
Sử dụng bộ dữ liệu khảo sat 200 học sinh về khối thì chính dự kiến sẽ thi (A-B-C-D) và giới tính.
Để xem toàn bộ nội dung bài viết, vui lòng truy cập link sau: https://ungdung.hotronghiencuu.com/kiem-dinh-tinh-doc-lap-cua-2-bien-dinh-danh
Ta đi kiểm tra xem có mối liên hệ nào giữa giới tính và khối thi hay không
Thao tác kiểm định Chi-square
Đưa các biến cần kiểm tra cào hàng và cột
Tại mục Statistics click vào Chi-square
Trên đây là thao tác cơ bản nhất. Tất nhiên nếu bạn muốn có các phân tích sâu hơn có thể click luôn các lựa chọn khác sẽ được đề cập ở phần tiếp theo.
Nhấn Continuce >OK để ra kết quả
Đọc kết quả
+ (1) phần mềm báo cáo không có ô nào có giá trị dự đoán dưới 5. Vậy giả định số 4 thoả mãn, kết quả kiểm định khi bình phương là phù hợp
+ (2) Giá trị chi-square quan sat =78.128, 3 bậc tự do. Sig <0.05 nên ta bác bỏ H0, vậy ta kết luận giữa giới tính và khối thi không độc lập (có liên quan đến nhau). Ở đây 3 bậc tự do thì 3= (2-1)*(4-1)
Như vậy kết luận chính trong bài kiểm tra tính độc lập đã xong. Tuy nhiên để có thể tưởng tượng thêm về cái “mối quan hệ” ấy ta có thể phân tích sâu hơn chút,với những bảng đơn giản (không phải lúc nào cũng có thể làm được và mô ta được rõ ràng nhé.
Tất nhiên nếu kiểm định kết luận rằng không có mối quan hệ thì ta không cần thiết phân tích sâu hơn nữa nhé.
Trung tâm Hỗ trợ nghiên cứu
Phone 24/7: 086 978 6862 (Mr Hùng)
Viết luận văn thuê trọn gói 0924 04 03 88 (Ms. Bông) Email: Bong.4388@gmail.com
Từ khóa: dịch vụ spss | phân tích spss | hỗ trợ spss | dịch vụ dữ liệu
***Dịch vụ SPSS- AMOS- SmartPLS***
Hotline, zalo: 086 978 6862.
Link zalo:https://zalo.me/0869786862
Quét mã QR để kết bạn ZALO.Vui lòng kết bạn trước khi nhắn tin. Để có phản hồi nhanh nhất hãy gọi thẳng số điện thoại bên trên 24/7
Nếu không thể tìm thấy zalo bạn có thể chat qua messeneger:https://www.messenger.com/t/manhhungdigi
Email: phantichso247@gmail.com
Xin vui lòng chú ý một số điều sau
- Các bạn có thể bình luận với tài khoản Google, tài khoản tùy chọn (tên, địa chỉ) hoặc ẩn danh
- Nếu thực sự quan tâm một chủ đề nào đó, khi bình luận xong hãy nhân vào nút "Thông báo cho tôi" ở góc dưới. Khi đó nếu có các bình luận và thảo luận mới về chủ đề này sẽ có thông báo gửi đến email của bạn
- Nếu cần hỗ trợ, hãy để lại số điện thoại. Nên chủ động gửi tài lệu về Hỗ Trợ Nghiên Cứu
- Các bình luận spam, có lời lẽ không phù hợp sẽ bị chặn
0 nhận xét:
Đăng nhận xét